Cuckoo Filter

比Bloom-filter更好的过滤器

     我们经常会遇到一个需求，就是判断一个元素是否在某个集合里面，首先想到的是维护一个HashMap（比如python中的字典），但是存储容量占比高，考虑到负载因子的存在，通常空间是不能被用满的，而一旦你的值很多例如上亿的时候，那 HashMap 占据的内存大小就变得很可观了，还需要存储对象的key（防止碰撞后没法确定元素），内存可能会装不下，我们需要一个空间效率更高的数据结构，这个时候我们一般会想到Bloom-filter。Bloom-filter可以看作k个hash函数+Bitmap，原理是通过k个hash函数将元素映射到Bitmap的k个位置，因为Bitmap只用1个bit就可以存储一个值，所以空间效率非常高，关于Bloom-filter，网络上已经有很多介绍的文章，就不赘述了。对于判断一个数据是否在某个海量数据的集合里面，Bloom-filter有奇效，比如应对缓存穿透、垃圾邮件的判断等
     但是Bloom-filter并不是完美的，比如Bloom-filter不支持删除，一旦需要删除一个元素，就只能重建Bloom-filter，简单的把元素hash后的k个位置置0会造成其他元素的误判（误判一个已经存在的元素为不存在，破坏了Bloom-filter的特性），对于此，有不少的Bloom-filter的变种，比如counting Bloom，d-left counting Bloom，大致的原理是把Bitmap位数组的每一位扩展为一个小的计数器。增加了实现复杂度的同时还降低了空间利用率，那有没有更好的替代方案呢？所以由此引入这次的主角：Cuckoo-Filter

Cuckoo Hash

     介绍Cuckoo-Filter之前得先说说Cuckoo Hash。Cuckoo Hash其实是一种解决hash冲突的策略。
     Cuckoo是布谷鸟的意思，也就是我们常说的杜鹃。“鸠占鹊巢”里面的“鸠”的就是类似杜鹃这种鸟类。这种鸟有一种即狡猾又贪婪的习性，它不肯自己筑巢，而是把蛋下到别的鸟巢里，而且它的幼鸟又会比别的鸟早出生，布谷幼鸟天生有一种残忍的动作，幼鸟会拼命把未出生的其它鸟蛋挤出窝巢，今后以便独享“养父母”的食物。借助生物学上这一典故，cuckoo hashing处理碰撞的方法，就是把原来占用位置的这个元素踢走，不过被踢出去的元素还要比鸟蛋幸运，因为它还有一个备用位置可以安置，如果备用位置上还有人，再把它踢走，如此往复。直到被踢的次数达到一个上限，才确认哈希表已满，并执行rehash操作，下图是一个Cuckoo Hash的例子：

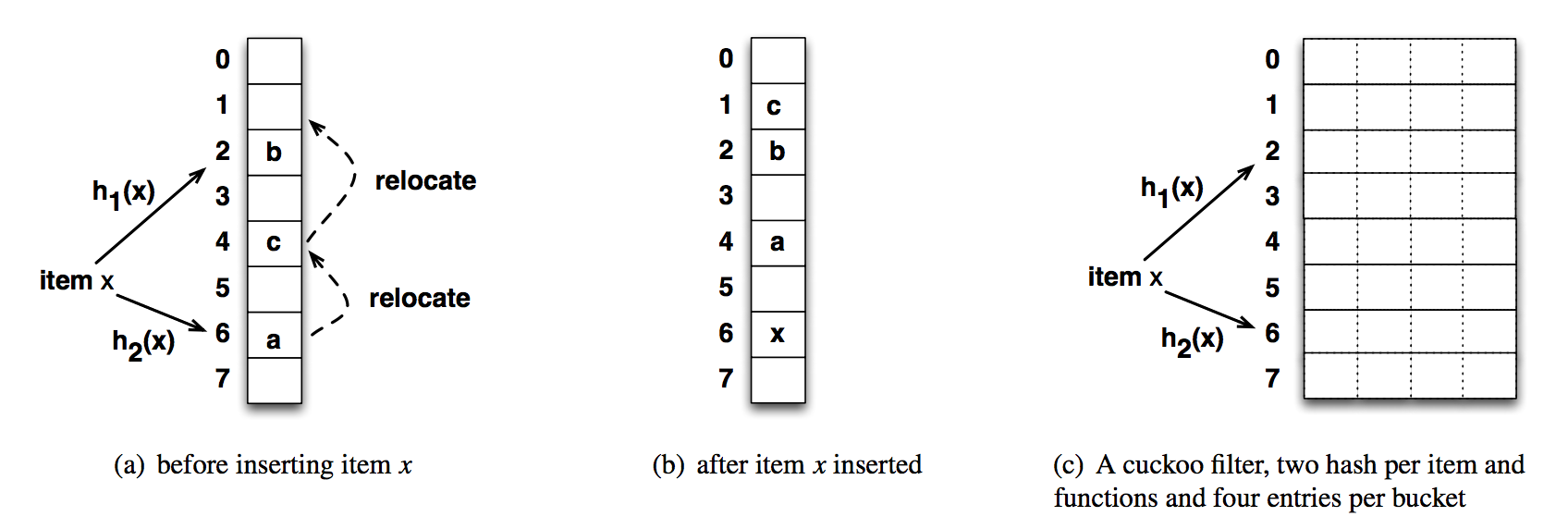
    Cuckoo hash会有多个hash函数（一般是两个），把一个元素x映射到多个位置上，这一点和Bloom-filter很像，但是Cuckoo hash只会在多个位置中选择一个空的位置来存储x（或其他信息，取决于实现）。如果都满了，就随机选一个位置“踢走”那个元素，把那个元素踢到它自己的替代位置上去，如果它的替代位置也满了，则继续踢。图中就是要插入一个x，发现hash后的两个位置都被占了，所以随机选择了6的位置踢走了元素a，a找到了自己的备用位置4发现已经被c占了，接着把c踢走，c最后找到了一个空的位置1，整个插入过程完成。      这样会造成一个问题，就是插入的开销会在元素越来越多的时候变得越来越大，元素可能会一直踢来踢去，甚至出现死循环，比如下图（极端情况）

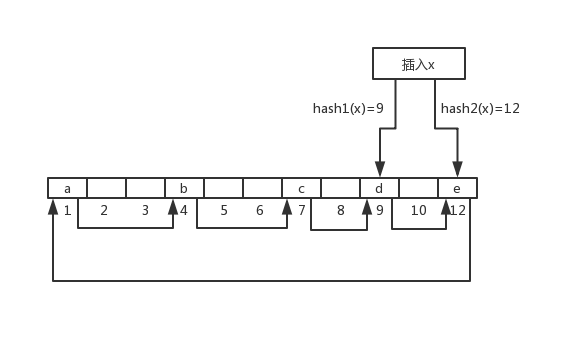
     元素x经过2个hash后的位置都被占了，随机选择一个位置12，把e踢走，e的备用位置被a占了，踢走a，a又踢走了b，b又踢走了c，c踢走了d，d的备用位置是12，于是又把刚插入的x给踢走了……陷入了死循环，所以需要一个上限，达到上限只能重建。此时可以衡量Cuckoo Hash的最大负载因子，负载因子 = 已经存入的元素 / 总的bucket。上图中这种可以看作只有一个slot的bucket，增加slot比如图c，可以大大减少冲突后踢走元素的概率，每个bucket对应一个hash值，相同hash值的元素都存在同一个bucket的不同slot中，除非2个bucket的8个slot都满了，否则不会踢元素。一维数组实现的cuckoo hash的负载因子大小和其他hash策略没什么区别，只有50%，但是多路slot的实现，比如图c中，能达到90%以上，可以说效率很高了。

Cuckoo-Filter设计

     本文主要参考了酷壳和CMU论文的实现，这篇论文首先提出了Cuckoo-Filter，很有参考价值。      论文中在Cuckoo-Filter的设计上比起基本的Cuckoo Hash有不少的优化。作为过滤器，空间肯定是能省就省，所以在每个slot中不会存原本的元素x，而是存的元素x的fingerprint(指纹，记做f)。由于存的是指纹，没有存x本身或者x的备用位置，或者那么在寻找元素的备用位置的时候怎么知道备用位置呢。作者采用了一种比较巧妙的办法，第一个地址用hash(x)来确定，第二个地址用hash(f)和第一个地址做异或来确定，这样不管当前是哪个地址，直接用当前地址和hash(f)做异或就可以得到另外一个地址。同时，插入的时候优先选择空的位置，而不是踢走其他的元素。
     刚开始其实还有一个比较疑惑的点，为什么求第二个地址的时候用的是hash(f)来异或呢，而不是直接异或f得到第二个地址，最后在论文中找到了答案(有些词不好翻译就直接贴原文了)：

In addition, the fingerprint is hashed before it is xor-ed with the index of its current bucket to help distribute the items uniformly in the table. If the alternate location were calculated by “i ⊕ fingerprint” without hashing the fingerprint, the items kicked out from nearby buckets would land close to each other in the table, if the size of the fingerprint is small compared to the table size. For example, using 8-bit fingerprints the items kicked out from bucket i will be placed to buckets that are at most 256 buckets away from bucket i, because the xor operation would alter the eight low order bits of the bucket index while the higher order bits would not change. Hashing the fingerprints ensures that these items can be relocated to buckets in an entirely different part of the hash table, hence reducing hash collisions and improving the table utilization.

     主要是因为fingerprint可能远小于hash(x)，直接异或fingerprint可能导致异或的只有地址1的低位，造成的结果是地址2可能就在地址1的附近，8位的fingerprint下地址1和地址2最大偏移距离只有256，两个地址产生了某种关联性，会加大产生冲突的可能（直接理解是没问题的，但是作者没有给出证明）
     除了上面说的这些，作者还做了一个优化来节约空间，称之为"Semi-sorting Buckets"。这种做法的前提是fingerprint在slot中的顺序不影响查询。具体的比如4个slot的bucket，每个slot中保存4位的fingerprint，那么bucket一共是16位。如果我们对4位的fingerprint进行排序，总共有3876种可能（??这个地方没怎么看懂，不知道这个数怎么出来的，留个坑），也就是16位的空间没有完全利用起来，3876<2^12，所以我们可以建立一个12位数值到这部分16位的值的映射。bucket只保存这个映射的key，也就是12位，每次对bucket的处理都相当于经过了一次解码编码的过程，时间上会造成一定的损耗，但是空间利用率更高了，16个bit的bucket节约了4个bit的空间，相当于3/4。
     下面会贴出插入、查找、删除的伪代码(来源论文，没有做Semi-sorting的bucket)：

    插入

f = fingerprint(x)
i1 = hash(x)
i2 = i1 xor hash(f)
if bucket[i1] or bucket[i2] has an empty entry then
    add f to that bucket
    return Done
i  = randomly pick i1 or i2
for n=0;n<MaxNumKicks;++n
    randomly select an entry e from bucket[i]
    swap f and the fingerprint stored in entry e
    i = i xor hash(f)
    if bucket[i] has an empty entry then
        add f to bucket[i]
        return Done
return Failure

首先计算了元素x的指纹f、两个地址i1和i2，然后查看i1和i2是否有空位，有的话直接插入，返回成功。没有的话随机挑一个踢出去，取踢出去的值赋给f，通过hash(f) xor i找到这个踢出去的元素的备用地址，再看是否被占用，没有的话直接插入，有的话重复上面一个过程，超过最大踢的次数就表明过滤器已经满了需要重建。

    查找

f = fingerprint(x)
i1 = hash(x)
i2 = i1 xor hash(f)
if bucket[i1] or bucket[i2] has f then
    return True
return False

查找的比较简单，计算出了两个地址，如果在两个slot中发现了指纹说明元素存在（有一定误判率，下面会分析）

    删除

f = fingerprint(x)
i1 = hash(x)
i2 = i1 xor hash(f)
if bucket[i1] or bucket[i2] has f then
    remove a copy of f from this bucket
return False

和查找一样，删除也有一定的误判率，如果在被删除元素的备选位置上，有个元素的备选位置是被删除元素的当前位置，并且它的指纹也和被删除元素一样，那么即使删除了当前元素，再找的时候也会产生误判这个元素还存在。

Cuckoo-Filter相关分析

    Cuckoo-Filter和Bloom-Filter一样，存在着一定的误判率，比如两个元素x、y，如果x、y的fingerprint一样都为f，而且同时hash(x) == hash(y) 或者 hash(x) == hash(y) ^ f 则过滤器根本无法分辨x和y，插入x，再查y发现y也存在，其实查到的是x。这种碰撞发生的概率叫做false positive(假阳率)，就是有可能判断一个并不存在的元素为存在，类似Bloom-Filter。另一方面，对于不存在的元素，肯定能返回不存在的结果。
    对Cuckoo-Filter来说，可以从这几个方面来衡量它的好坏，一个是空间利用率，一个是插入、查找、和删除的时间开销。
    在计算空间利用率之前，可以先设置相关的变量。这里我们沿用作者的设定：

     ε表示我们期望达到的过滤器的错误率，f表示指纹的长度（bit），α表示负载因子（load factor），b表示每个bucket的slot的数量，m表示过滤器中一共有多少个bucket，n表示我们要插入的item的总数，C表示的平均每个item占用的bit数。我们要计算的就是C，代表的其实就是Cuckoo-filter的空间效率。

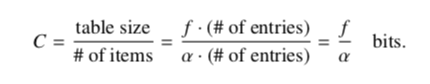
    那么这个值怎么算呢，平均每个item的大小(bit)=过滤器的总的大小(bit)/插入的item的数目，最后化简得到f/α。也就是说明和指纹长度成正比，和负载因子成反比。说明负载因子越大，空间效率越高，这个好理解。同时指纹长度越小，空间效率越高，那指纹长度能不能无限小呢？当然不行，比如求出了一个地址hash(x)，那备用的地址就只有f ^ 2种可能，指纹长度越小，碰撞的概率就越大，间接的影响了负载因子的大小，作者在论文中表明了这种影响。
    除此之外，还有一个约束条件，就是我们期望的错误率ε。错误率我们怎么和指纹长度联系起来呢？错误率其实就是把一个没在过滤器中的元素给误判成在存在的概率

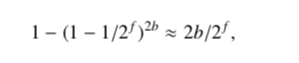
    上图是计算错误率的公式，比如插入x，hash(x)得到第一个bucket的位置，这个bucket和备用bucket一共有2b个元素。和其中某个元素指纹相同的概率为1/2^f，先计算出和2b个元素指纹不碰撞的概率，然后用1减去不碰撞的概率得到就是错误率。

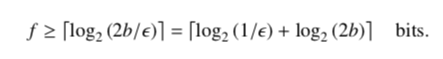
    代入期望达到的错误率ε，得到指纹长度的下界。这里表明了一个问题，越大的cuckoo-filter为了保持一定的错误率，需要越大的指纹长度，否则错误率将增加。

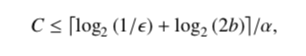
    和上面计算空间效率的公式结合，可以得到这个公式，指明了我们期望的错误率越小或每个bucket的slot数目越大则平均每个item的空间损耗的上界越大。

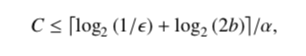
    查找的时间消耗。查找一个元素，最多会查找2b次，删除也是，可以认定为O(1)的时间复杂度。插入元素的时间复杂渐进为O(1)，在前期bucket没满的时候，直接插入即可，满了就开始踢元素，当负载因子增加的时候，插入的时间将来越久，最终超过最大的踢的次数就只能重建了，时间复杂度的具体证明见原论文。

Cuckoo-Filter和Bloom-Filter对比

    Cuckoo-Filter对比Bloom-Filter，最主要的就是支持删除，虽然counting Bloom也支持删除，但是空间利用率又远远不如Cuckoo-Filter。在空间利用率上，原论文给出了对比：

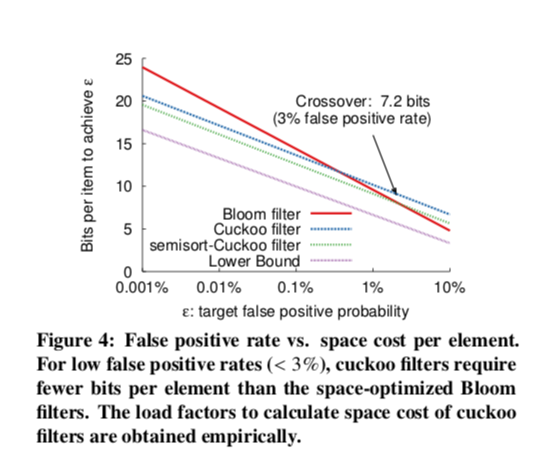
    上面我们讨论过，Cuckoo-Filter的空间效率和我们预定的错误率是有关系的，Bloom-Filter也是这样的，从图中可以看到，当错误率小于3%的时候，semisort-Cuckoo Filter的空间效率是比Bloom-Filter要高的，即使是不是semisort优化的普通Cuckoo，在图中可见的0.1%错误率以内，也是要比Bloom-Filter空间效率要高。而在实际使用中，我们一般不会容忍这么高的错误错误率，所以实际上来说Cuckoo-Filter的空间性能要更好一点。
    时间性能上，两者的查找都是常量时间复杂度，但是如果数据集过于巨大以至采取了持久化的策略，则Cuckoo-Filter要优于Bloom-Filter，因为最多只需要读取两个bucket，而Bloom-Filter则需要读K次。对于插入，Cuckoo-Filter在负载因子较大的时候因为会踢数据，所以可能会比Bloom-Filter更慢，甚至出现插入失败的情况，这种时候就只能重建了。而Bloom-Filter的插入不会受到负载因子的影响，另外，它还有跟Bloom-Filter共有的一个缺点，就是访问空间地址不连续，通常可以认为是随机的，这样严重破坏了程序局部性，对于Cache流水线来说非常不利。
    关于两者对比的更多的讨论可以查看这个问题：https://stackoverflow.com/questions/867099/bloom-filter-or-cuckoo-hashing
    综上，Cuckoo-Filter是一种很优秀的数据结构，但是目前相关的工程化的应用还不是特别多，不过这也给了我们机会去实现一个更高效的轮子。

参考链接

• https://www.cs.cmu.edu/~dga/papers/cuckoo-conext2014.pdf
• https://coolshell.cn/articles/17225.html
• https://brilliant.org/wiki/cuckoo-filter/
• https://stackoverflow.com/questions/867099/bloom-filter-or-cuckoo-hashing
• http://legendtkl.com/2017/07/23/about-hash-table/
• https://www.cnblogs.com/chuxiuhong/p/8215719.html